Álgebra: Teoria dos Números: Inteiros

Se nós estendermos acrescentando 0 podemos chegar a noção de uma

• identidade para a adição, dada por:          
  

  Afirmando que existe um número 0, que somado a um número natural dá o próprio número.

Aqui temos uma escolha a fazer, onde em nossa ordenação se encaixa o 0? A escolha usual é 0 < 1 e é o que vamos fazer aqui, mas vale a pena salientar a curiosa natureza desta escolha. Tendo definido zero, a possibilidade de uma inversão de surge, que denota o conjunto de inversas como 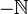satisfazendo o seguinte axioma.

• Inverso Aditivo
  

  .

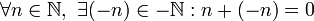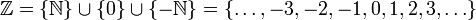Combinando os três obtemos os inteiros . Os inteiros nos permitem acompanhar as dívidas, bem como contar as coisas, em outras palavras, para realizar contagem. Se você assumir que os axiomas estão bem ordenados assumindo a forma

• .

E que a identidade, fechamento e distributividade da multiplicação para segurar os inteiros então a operação multiplicação também pode ser expandida para incluir todos os inteiros
Eles podem ser construídos facilmente a partir dos números naturais. Eles podem ser cada classe de equivalência de pares ordenados (a, b) onde a e b são dois números naturais. Em seguida, pode-se dizer que (a, b) e (c, d) são iguais quando a + d = b + c, a soma (a, b) + (c, d) = (a + c, d + b). E o produto (a, b)(c, d) = (ac + bd, ad + bc), onde as definições da soma e produto de números naturais são utilizados. Existe uma identidade aditiva(elemento) na forma (a, a) porque (a, a) + (b, c) = (a + b, a + c), o que é equivalente a (b, c) porque a + b + c = a + b + c. Todos estes elementos da forma (a, a) são obviamente equivalentes. Todos os elementos (a, b) tem um inverso aditivo (b, a) porque (a, b) + (b, a) = (a + b, a + b). A melhor maneira de pensar destes pares ordenados (a, b) é de pensar como eles a-b. Assim, (a, a) podem ser consideradas como "0".